In an earlier article, I described how to measure transmitter power output using an in-line directional wattmeter. That same wattmeter can also measure the voltage-standing-wave-ratio or VSWR on the transmission line. The VSWR can be deduced by the measuring the forward power Pfwd and reverse power Prev, then calculating VSWR according to the relationship:
VSWR = [1 + (Prev/Pfwd)0.5] / [1 - (Prev/Pfwd)0.5]
The value (Prev/Pfwd)0.5 is also known as the reflection coefficient, Psi or ψ. This simplifies the VSWR calculation to
VSWR = (1 + ψ) / (1 - ψ)
For example, if we measure forward power at 22-Watts and reverse power at 2-watts, we have a reflection coefficient of
ψ = (2/22)0.5 = 0.30
The VSWR is then
VSWR = (1+0.30)/(1−0.3)
VSWR = 1.3 / 0.7
VSWR = 1.85
A further consideration is the distance between the antenna and the wattmeter and the effect of any loss in the transmission line. In a typical small boat installation there is a length of coaxial transmission line from the antenna, and that is the point in the circuit the wattmeter will be inserted. On a small boat the transmission line is likely to be RG-58C/U and be 15-feet long. We must consider the effect of attenuation in that transmission line on the measurement of the antenna VSWR.
First we must calculate the loss in the transmission line. As mentioned previously, RG-58C/U will have a characteristic attenuation of 6.2 dB in 100-feet. Thus in 15-feet the attenuation will proportionally be 0.945 dB.
In our test set up, the wattmeter is placed 15-feet away from the antenna. If we measured 22-Watts at the wattmeter location, that power will be attenuated by 0.945 dB by the time it reaches the antenna. We must calculate the actual power at the antenna as being 0.945 dB lower. Again we use the relationship
dB = 10 log10 (P2/P1)
and insert the known values, -0.945 dB and P1 = 22 watts. Solving we get
P2 = 17.7 Watts
This is the actual power that reached the antenna, only 17.7-Watts, due to transmission line loss in the 15-feet of RG-58C/U. This value is our actual Pfwd for the VSWR calculation.
At the antenna some portion of this 17.7-Watts will be reflected back toward the transmitter. The reflected power will also be attenuated in the transmission line by 0.945 dB. We know that after attenuation, there was 2-Watts of power at the wattmeter, but we need to know how much reverse power was at the antenna, which will be 0.945 dB greater. Again we use the relationship of two powers and the known ratio between them in dB to find the actual reverse power at the antenna, in this case 2.49-Watts.
Now we can calculate the actual VSWR at the antenna, using
Pfwd = 17.7-Watts
Prev = 2.49-Watts
First we find the reflection coefficient, ψ
ψ = (2.49/17.7)0.5 = 0.375
Then we compute the VSWR
VSWR = (1+0.375)/(1−0.375)
VSWR = 1.375 / 0.625
VSWR = 2.2
Now we have an accurate measurement of the VSWR of the antenna at its feed point. The actual VSWR at the antenna is 2.2, quite a bit higher than the measured VSWR of 1.85 at a point 15-feet away on the transmission line. Note that any transmission line loss will always tend to make the antenna VSWR appear better (lower) that the actual VSWR at the antenna.
A further compounding of this calculation is to adjust the transmission line attenuation to include an allowance for the influence of a high VSWR on the transmission line. For all practical transmission lines, the presence of any standing waves on the transmission line (that is a VSWR greater than 1) causes the attenuation in the transmission line to increase. In the analysis above, we have ignored that effect.
Measuring Radio Antenna VSWR
Re: Measuring Radio Antenna VSWR
To calculate the total loss in a transmission line where there are standing waves present, we first define two new parameters in terms of already known parameters:
If
ML = rated loss of cable without standing wave in decibels, called matched loss
VSWR = voltage standing wave ratio
then define
|ρ| = (VSWR-1)/(VSWR+1)
and
α = 10ML/10
Find TOTAL LOSS from
Total Loss (dB) = 10 log [ ( α2 - |ρ|2) / (α(1-|ρ|2) ]
For example, with a transmission line having a matched loss of -2dB and and a true VSWR at the antenna of 3, the total loss would be:
|ρ| = (VSWR-1)/(VSWR+1)
|ρ| = (3-1)/(3+1)
|ρ| = (2)/(4)
|ρ| = 0.5
α = 10ML/10
α = 10-2/10
α = 0.63
Solving for TOTAL LOSS gives -5 dB, substantially more than the matched loss of -2 dB.
Cf.: http://www.astrosurf.com/luxorion/Radio/effect-load-vswr.pdf
If
ML = rated loss of cable without standing wave in decibels, called matched loss
VSWR = voltage standing wave ratio
then define
|ρ| = (VSWR-1)/(VSWR+1)
and
α = 10ML/10
Find TOTAL LOSS from
Total Loss (dB) = 10 log [ ( α2 - |ρ|2) / (α(1-|ρ|2) ]
For example, with a transmission line having a matched loss of -2dB and and a true VSWR at the antenna of 3, the total loss would be:
|ρ| = (VSWR-1)/(VSWR+1)
|ρ| = (3-1)/(3+1)
|ρ| = (2)/(4)
|ρ| = 0.5
α = 10ML/10
α = 10-2/10
α = 0.63
Solving for TOTAL LOSS gives -5 dB, substantially more than the matched loss of -2 dB.
Cf.: http://www.astrosurf.com/luxorion/Radio/effect-load-vswr.pdf
Re: Measuring Radio Antenna VSWR
Regarding the characteristic loss in RG-58C/U transmission line, I use the BELDEN 8262 cable as a typical type. From the specification sheet we get loss data as follows:
100-MHz = -4.9 dB/100-feet
200-MHz = -7.3 dB/100-feet
Interpolating I get a figure
156-MHz = -6.2 dB/100-feet
To get a figure for a length of 15-feet, the loss is figured with direct proportion:
-6.2 dB/100-feet × 15-feet = -0.94 dB
100-MHz = -4.9 dB/100-feet
200-MHz = -7.3 dB/100-feet
Interpolating I get a figure
156-MHz = -6.2 dB/100-feet
To get a figure for a length of 15-feet, the loss is figured with direct proportion:
-6.2 dB/100-feet × 15-feet = -0.94 dB
Re: Measuring Radio Antenna VSWR
Regarding VSWR measurement of antennas for the VHF Marine Band, the measurements should be made over a range of transmit frequencies. The typical radio for a ship station will be able to transmit on the following frequencies (with the channel number shown in parenthesis):
156.050 (1)
156.250 (5)
156.450 (9)
156.650 (13)
156.800 (16)
157.000 (20)
157.200 (24)
157.400 (28)
Note: in the USA band plan, a radio cannot transmit at full power on 156.850 (17); it is a 1-Watt channel. We use 156.800 (16) instead.
Plotting the VSWR at these eight test frequencies should reveal the antenna tuning and the approximate frequency of lowest VSWR. Here is an example of a plot of VSWR v. Frequency for a typical VHF Marine Band antenna, the GAM SS-2.
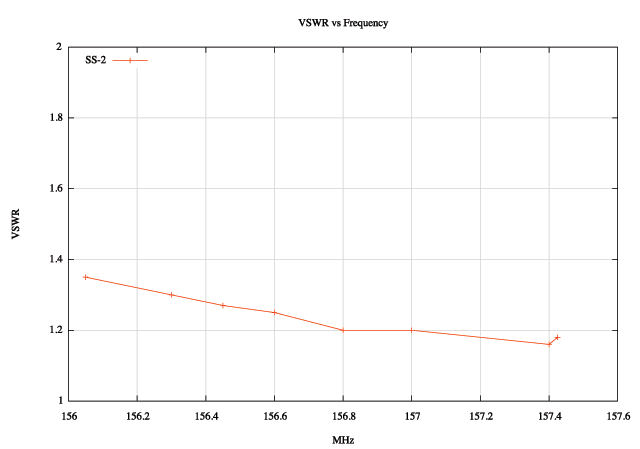
For many VHF Marine Band antennas encased in a fiberglass radome, there is no possibility of making an adjustment to the length of the radiating element to improve tuning of the antenna. For end-fed half-wavelength antennas using small-diameter metal rods for the radiating element, the length can be adjusted. Antennas with metal rod whips are, generally, sold already tuned and the rod length cut for the lower end of the band. Any shortening of the radiator should be done with caution; once you cut off too much of the rod you cannot easily go back to a longer length.
Note that attempting to tune an antenna for use with an AIS transmitter by using a typical VHF Marine Band radio as a signal source will be very difficult. The typical ship station radio cannot transmit on the AIS frequencies, channels 87B (161.975-MHz) and 88B (162.025-MHz). Using a standard ship station radio and directional wattmeter, it will be impossible to measure the VSWR of an antenna at AIS frequencies.
156.050 (1)
156.250 (5)
156.450 (9)
156.650 (13)
156.800 (16)
157.000 (20)
157.200 (24)
157.400 (28)
Note: in the USA band plan, a radio cannot transmit at full power on 156.850 (17); it is a 1-Watt channel. We use 156.800 (16) instead.
Plotting the VSWR at these eight test frequencies should reveal the antenna tuning and the approximate frequency of lowest VSWR. Here is an example of a plot of VSWR v. Frequency for a typical VHF Marine Band antenna, the GAM SS-2.

For many VHF Marine Band antennas encased in a fiberglass radome, there is no possibility of making an adjustment to the length of the radiating element to improve tuning of the antenna. For end-fed half-wavelength antennas using small-diameter metal rods for the radiating element, the length can be adjusted. Antennas with metal rod whips are, generally, sold already tuned and the rod length cut for the lower end of the band. Any shortening of the radiator should be done with caution; once you cut off too much of the rod you cannot easily go back to a longer length.
Note that attempting to tune an antenna for use with an AIS transmitter by using a typical VHF Marine Band radio as a signal source will be very difficult. The typical ship station radio cannot transmit on the AIS frequencies, channels 87B (161.975-MHz) and 88B (162.025-MHz). Using a standard ship station radio and directional wattmeter, it will be impossible to measure the VSWR of an antenna at AIS frequencies.
Re: Measuring Radio Antenna VSWR
Previously I wrote:
For readers whose use of logarithms is a bit rusty, I will show the derivation in detail. First we define the variables:
P1 = the power measured at the transmitter, 22-Watts
dB = the loss calculated to occur in the transmission line expressed in deciBels, -0.945
P2 = the power that will arrive at the antenna, which is to be solved for.
These three variable are related by the basic equation for definition of the deciBel for comparison of two power levels:
dB = 10 log10 (P2/P1)
Note that the logarithm is base=10.
From algebra we then rewrite that relationship to
dB/10 = log10(P2/P1)
From the definition of logarithms we then rewrite
10dB/10 = P2/P1
From algebra we finally rewrite to find P2
P2 = (P1 × 10dB/10)
Solving for P1 = 22-Watts, and dB = -0.945, we substitute the known values:
P2 = (22-Watts × 10-0.945/10)
P2 = (22-Watts × 10-0.094)
P2 = (22-Watts × 0.804)
P2 = 17.7-Watts
I find it helpful to show all the steps when handling problems involving decibels due to the use of logarithms, which often confuse readers who don't deal with them all the time.
...In our test set up, the wattmeter is placed 15-feet away from the antenna. If we measured 22-Watts at the wattmeter location, that power will be attenuated by -0.945 dB by the time it reaches the antenna. We must calculate the actual power at the antenna as being -0.945 dB lower. Again we use the relationship
dB = 10 log10 (P2/P1)
and insert the known values, -0.945 dB and P1 = 22 watts. Solving we get
P2 = 17.7 Watts...
For readers whose use of logarithms is a bit rusty, I will show the derivation in detail. First we define the variables:
P1 = the power measured at the transmitter, 22-Watts
dB = the loss calculated to occur in the transmission line expressed in deciBels, -0.945
P2 = the power that will arrive at the antenna, which is to be solved for.
These three variable are related by the basic equation for definition of the deciBel for comparison of two power levels:
dB = 10 log10 (P2/P1)
Note that the logarithm is base=10.
From algebra we then rewrite that relationship to
dB/10 = log10(P2/P1)
From the definition of logarithms we then rewrite
10dB/10 = P2/P1
From algebra we finally rewrite to find P2
P2 = (P1 × 10dB/10)
Solving for P1 = 22-Watts, and dB = -0.945, we substitute the known values:
P2 = (22-Watts × 10-0.945/10)
P2 = (22-Watts × 10-0.094)
P2 = (22-Watts × 0.804)
P2 = 17.7-Watts
I find it helpful to show all the steps when handling problems involving decibels due to the use of logarithms, which often confuse readers who don't deal with them all the time.