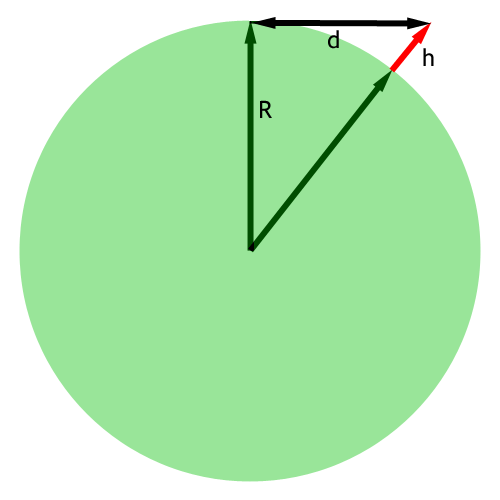
Figure 1. Earth radius, height of observer, and distance to horizon. The scale of the typical height of observer is greatly exaggerated in this sketch.
A careful look is taken at the notion of a radio horizon and its calculation. Rather than just give a formula, its derivation is shown and explained.
The distance to the horizon varies with the height of the observer, or in the case of radio, with the height of the radio's antenna. There is a well-known formula for calculating the radio horizon which says the distance in miles will be the square-root of twice the height in feet. When I see a formula, I tend to be curious about how it was derived. This curiosity led me to derive the formula, which I show below.
The geometric distance to the horizon from a particular height above the Earth is illustrated below:

Figure 1. Earth radius, height of observer, and distance to horizon. The scale of the typical height of observer is greatly exaggerated in this sketch.
R is the radius of the Earthh is the height of the observer or antennad is the distance to the horizonThe three lines form a right triangle, and by Pythagorean theorem, we can say
d2 + R2 = (R + h)2
We can evaluate this and solve for distance d:
d2 = (R + h)2 - R2
= R2 + 2Rh + h2 - R2
= 2Rh + h2
d = (2Rh + h2)0.5
In the case of the Earth radius R and of the typical observer or antenna height h, we see that R is very much greater than h. For example:
Earth radius = 20,902,253-feet
height = 10-feet
Because of this we can simplify our calculation. The value for h2 will be extremely small compared to 2Rh. For example, at a height of 10-feet, the Earth radius is larger by a factor of more than 2,000,000:1. If we look at the relationship,
d2 = 2Rh + h2
is really the same as
d2 = h(R + R + h)
If we ignore adding that final h, which is extremely small in comparison to the two R terms there will not be much effect on the product. Thus we can say that the approximate relationship is:
d2 = 2Rh
d = (2Rh)0.5
Since we know the Earth radius, we can include its value in the formula. Because we will be working with the height in feet, we will need to use the same units for the Earth radius. The Earth is not a perfect sphere. Its radius at the equator is different than at the poles. We can use a value that is accepted as the mean Earth radius, which is 3,958.76-miles or 20902252.8-feet (or 6371-kilometers). The distance-to-horizon formula then reduces to
d = (2 x 20902252.8 x h)0.5, where d and h are in feet
We can evaluate this further and have
d = (41804505.6 x h)0.5, where d and h are in feet
By the law of square roots, we can also say
d = (41804505.6)0.5 x h0.5
d = 6,465.64 x h0.5
It is more convenient to have the distance to the horizon in miles, so we can divide by 5,280 (the number of feet in a mile) and get the familiar relationship
d = (6465.64 / 5280) x h0.5
d = 1.22 x h0.5 where d is in miles and h is in feet
We now have the geometric distance to the horizon from an observer or antenna of a certain height. The optical horizon will be slightly different due to refraction of light in the atmosphere. The density of the atmosphere is not completely uniform, and as light travels through the atmosphere it passes through layers of different density. This causes the light to be refracted.
The esteemed nautical reference work, AMERICAN PRACTICAL NAVIGATOR by Bowditch has considered this problem. As one might expect, it had quite a bit to offer on the subject. Bowditch provides a collection in their TABLE 12 of the distance to the (optical) horizon from various heights of eye. It notes that the actual distance will vary somewhat with changes in atmospheric refraction, but that this variation is likely to be less than variations due to differences in the atmosphere from standard atmospheric conditions for temperature and pressure. The table is calculated from the formula
d = [ (2Rh) /( 6076.1 x βo) ]0.5
where:
R = the radius of the earth in nautical miles, or 3440.1
h = height of eye in feet
βo = 0.8279, a parameter that characterizes
the effect of terrestrial refraction, and
6076.1 = the number of feet in a nautical mile, used for conversion
Bowditch notes that this relationship simplifies to
d = 1.17 x h0.5 with d in nautical miles and h in feet
Conversion to statue miles yields
d = 1.345 x h0.5
We now have reasonably good formula for the distance to the geometric horizon or to the optical horizon as a function of the height. The optical horizon calculation was derived with the assumption that there was a certain refraction of light in the atmosphere. With radio waves, there is almost always more refraction occurring. This causes the radio horizon to be more distant than the optical horizon. The usual assumption for radio wave refraction is to describe the behavior as if the Earth radius were larger than it actually is by a factor of 4/3. This is called the four-thirds Earth effect or rule of thumb. We can easily apply this to our calculation. All that has to be done is to increase the value we use for the Earth radius by a factor of 4/3. Instead of using 20902252.8-feet as the Earth radius, we use 27869670.4. Using this value in the calculation produces:
d = (2 x 27869670.4 x h)0.5, where d and h are in feet
We can evaluate this further and have
d = (55739340.8 x h)0.5, where d and h are in feet
By the law of square roots, we can also say
d = (55739340.8)0.5 x h0.5
d = 7465.87 x h0.5
It is more convenient to have the distance to the horizon in miles, so we can divide by 5,280 and get the familiar relationship
d = (7,465.87 / 5,280) x h0.5
d = 1.414 x h0.5 where d is in miles and h is in feet
Because 1.414 happens to be the square-root of 2, this formula is often expressed as
d = (2 x h)0.5 where d is in miles and h is in feet
There we have it: the distance in miles to the radio horizon will be the square-root of twice the antenna height in feet. This calculation is an approximation, and it is based on the assumption of the 4/3-factor for refraction.
In the case of a small boat, we would expect the antenna height to be not more than about 10-feet. Our calculation then suggests that two such boats will have a radio horizon of 4.5-miles. Their radio horizons will just overlap at a maximum distance of about 9-miles apart. This implies they ought to be in range of radio communication with each other when about 9-miles or less apart. This range is typically obtained with ease with 25-watts of power in the transmitter.
The assumption of radio wave refraction behaving according to the 4/3-rule is an approximation for normal conditions. The refraction of radio waves is influenced by atmospheric conditions, and in some cases the refraction may be greater, and, as to be expected, in some conditions less. Atmospheric temperature layers, water content, and stillness all influence refraction.
DISCLAIMER: This information is believed to be accurate but there is no guarantee. We do our best!
Copyright © 2013 by James W. Hebert. Unauthorized reproduction prohibited!
This is a verified HTML 4.01 document served to you from continuousWave
Author: James W. Hebert
This article first appeared January 20, 2013.