by James W. Hebert
This article will examine three areas of boat propulsion. First, the propeller and its power requirements will be investigated. Next a hypothetical two-stroke-power-cycle engine's power curve will be compared to a known propeller's power curve. Finally, a hypothetical four-stroke-power-cycle engine's power curve will be compared to the propeller's curve.
Boat speed is a function of the speed at which the boat's propeller is turned, the size of the propeller, and the arrangement of its blades. It seems clear that a larger propeller, with more blades, and blades with a more aggressive bite will require more power to be turned. For a propeller of a given size, on a particular boat, the horsepower needed to turn the propeller is a function of how fast the propeller is turned. This relationship can be shown in a graph, and we call that function the propeller power curve.
Reference books on naval architecture give a formula for the propeller power curve, but fail to explain exactly how it was derived. When I see something like that, I like to apply my own knowledge and analysis to it to see see if I can derive the relationship myself from what I generally know about how boat speed and horsepower are related. Here is my analysis and derivation of the propeller power curve.
I will use the variables HP for power, RPM for propeller shaft speed, MPH for boat speed, and state this relationship mathematically with
(1) HP = (f)RPM
Now we just have to determine what the exact relationship happens to be.
We already have a sense of how these two parameters are related from the speed prediction formula used by Crouch. We know that RPM is going to be related directly to boat speed, and Crouch has describe a relationship between power and boat speed. Crouch's formula is
(2) MPH = C x (HP/LBS)0.5 where C is a constant unique to a particular hull
We can rewrite that relationship to isolate the HP term:
(3) HP = (LBS/C2) x MPH2
The first term (LBS/C2) reduces to a constant for a particular boat, so we can then say
(4) HP = some constant X MPH2
This gives us a relationship between propeller shaft power and boat speed, but we are looking for a relationship between propeller shaft power and propeller shaft speed. Fortunately, we also know a function that describes how boat speed is related to engine crankshaft speed:
(5) MPH = RPM x (PITCH/(RATIO X 1056)) x (1 - (SLIP/100))
The middle term (PITCH/(RATIO X 1056)) is a constant for a particular propeller and engine gear reduction ratio, so we can rewrite as
(6) MPH = RPM X (some constant) X (1 - (SLIP/100))
We also know that SLIP is itself a generally an inverse function of RPM. It tends to be high at low RPM and to decrease as RPM increases. So we can describe slip as a function of RPM
(7) SLIP = (f)RPM
We can substitute this equation (6) to get:
(8) MPH = RPM x (some constant) X (f)RPM
We have the term RPM in our equation more than once, so we can combine them:
(9) MPH = (RPM X (f)RPM) X (some constant)
Now we can use equation 9 to substitute for the term MPH in equation 4:
(10) HP = (some constant) X [(RPM X (f)RPM) X (some constant)]2
We can combine the constants into one term:
(11) HP = (some constant) X [(RPM X (f)RPM)]2
If we look closely at the RPM term we can see that at a minimum the term will simplify to
(12) RPMn where n = 2 or greater
Thus we can describe propeller shaft horsepower as being defined to be
(13) HP = C X RPMn where n = 2.0 or higher and C is a constant
Determining the exact value of n will require careful analysis of the individual hull and propeller. Fortunately, naval architect Dave Gerr tells us that experience has shown that n will range from about 2.2 to 3.0, and that for an average boat a value of n = 2.7 can be used. Thus we can say that the horsepower needed to turn a propeller on an average boat varies as a function of the RPM according to
HP = C X RPM2.7 where C is some constant for a specific hull and propeller combination
Gerr provides this formula in his PROPELLER HANDBOOK as Formula 1-2 on page 4, however he does not show any derivation of it. This somewhat "backdoor" derivation of it provides some insight into why the variables are related as they are.
If you are still following along in this derivation, you may now quite rightly ask how one derives the constant C. The answer: it is chosen arbitrarily to make the propeller power curve meet the engine horsepower curve at maximum RPM. You can't really measure it, you just have to deduce it from observation. Let's explore how we can deduce the constant C for a particular boat and propeller combination.
I have collected data about the performance of my own boat, and we can use that data to determine and plot a propeller power curve for my boat and propeller. We'll make two assumptions: that when the engine reaches its wide-open throttle speed (which is within the cited range of the full-power rating) it is delivering its rated 225-HP, and that the value of n is 2.7 (as suggested by Gerr as a good average value to use). (We really don't know precisely what is the horsepower being delivered by the engine to the propeller at other speeds, so we hope for the best with WOT and full rated power.) The propeller is an OMC three-blade SST with 15-inch pitch. It's my favorite all-around propeller on the boat.
To plot the curve, we have to find the constant C. We take the rated horsepower, 225, and the maximum RPM that can be reached with this propeller, 5900, and use them to determine C from the relationship
HP = C X RPM2.7
Solving this for C we have
(14) C = HP / RPM2.7 C = 225 / 59002.7 C = 1.48 X 10-8
Using 1.48 X 10-8 as a value for C, we then compute a table of horsepower needed to turn the propeller at each engine RPM according to equation 14 above:
RPM HP 1000 1.9 1500 5.6 2000 12.1 2500 16.8 3000 36.1 3200 43 3500 55 4000 78.7 4500 108 5000 155 5500 186 5750 210 5900 223
We plot these points to see the propeller horsepower curve

We now have a reasonable curve of how much horsepower it will take to turn the OMC SST 15-inch pitch propeller on my boat at a particular speed (shown in terms of engine crankshaft speed). The next step is to discover how much power is available from a engine to turn the propeller.
For any particular engine, the horsepower output will be proportional to the engine speed. Generally horsepower increases with engine speed, although in some cases, at the very highest engine speed, horsepower output actually decrease slightly, depending on the design of the engine.
I don't know of any general formula for describing the power output of an engine as a function of its crankshaft speed. Typically the manufacturer will publish that information. Unfortunately, for most outboard engines there is no published curve of horsepower output as a function of engine speed. However, there are a few engines which have such data published. Here is a plot of engine power output as a function of engine speed for several current outboard engines.
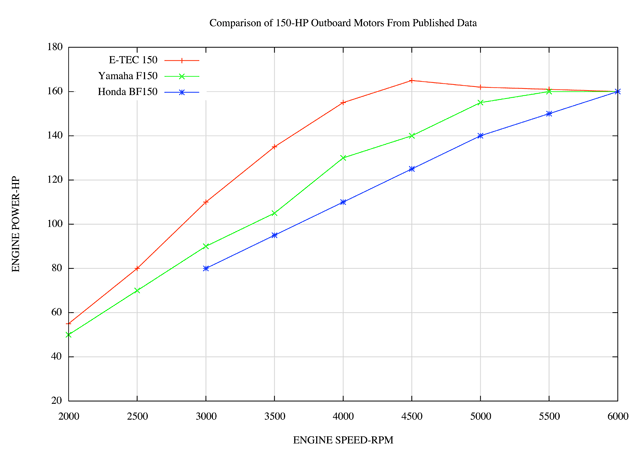
We can use the general shape of these power curve as a guide, and scale it to the horsepower (225) being used here. Since my engine is a two-cycle, I will use the shape of the power curve from the E-TEC 150 as a guide. It would be much more interesting if we could get these power curves from the manufacturer for every engine, but, sadly, outboard engine manufacturers seem very reluctant to publish this information. So we just have to go with an educated guess about what a particular engine's power curve might be. That's what I am doing here.
Now for the interesting part of this presentation, and sorry it took so long to get to it. Let's combine the two curves into one graph. The green line shows the power available from the engine, the red line shows the power needed by the propeller.

This plot shows that throughout the engine speed range the engine always is able to produce more power than the propeller requires. The plot also shows that the engine can continue to accelerate until the propeller power curve meets the engine power curve. At that engine speed the engine can no longer accelerate and has reached its maximum engine speed under the propeller's load.

To better show the reserve of power the engine has at most engine speeds, I have shaded the region in the plot (above).
With the boat set up with this propeller and engine combination, the performance ought to be very good. At all speeds there should be immediate acceleration and the engine should be very responsive. There is plenty of reserve power for situations where the load increases, either due to loading of more weight or to dynamic factors, such as encountering head seas. With this type of set up the engine speed will remain very steady at a particular throttle setting, and the engine will not hunt for a new speed if there is a change in loading (say due to wave conditions) which might overwhelm the engine's reserve. In general, this is an optimum configuration for good handling.
The only parameter not optimized in the set up shown above is probably fuel economy. If a propeller with greater pitch were used, its power curve would increase more rapidly, and it would rise to meet the engine power sooner. This would result in a lower maximum RPM for the engine. The general effect would be to reduce the shaded area of the curve where the engine has excess power. This will improve the fuel economy (because turning a higher pitch propeller tends to always improve the fuel economy), but it will reduce the reserve power available, reduce the ease of accelerating the boat, and also make the engine run harder at all speeds.
If the engine power curve is different, the amount of reserve power available will be different. Using the general shape of the power curve from the Honda BF150 engine, I scaled it to 225-HP and plotted it against the power curve for my propeller. Here is the result.

Again, these are somewhat hypothetical results, since I don't have the actual data for either of these engines. However, I think the general shape of the power curves is probably valid. In comparing the two plots, it is clear that with the four-cycle engine there is not as much reserve power available throughout the operating range. This will tend to make this combination have slower acceleration, less reserve power, and be more sensitive to added loads (from either added weight on board or from dynamic loads from head seas). The four-cycle engine also seems to be operating under generally higher loading at any given engine speed.
A reasonable derivation for the generally accepted propeller power curve has been demonstrated. No claim is made that the derivation is entirely valid, but its result is in good agreement with expert opinion. The average value of n =2.7 has been used to develop a propeller power curve based on actual observed data from my own boat. This curve has then been compared with two hypothetical engine power curves which are representative of two general types of outboard engines. The plotted data which resulted seems to be in general agreement with first-hand observations of the performance of boats, engines, and propellers of this type, which lends additional validity to the analysis and method.
If you have a question about this article, please post it to the message thread in the PERFORMANCE forum reserved for that purpose.
I thought it might be interesting to investigate the influence of the factor n in the propeller power curve equation. As mentioned above it is suggested that it tends to vary from 2.2 to 3.0, with 2.7 being an average value. With that in mind, here is a plot of my SST 15-inch propeller power curve with three different values of n assumed.
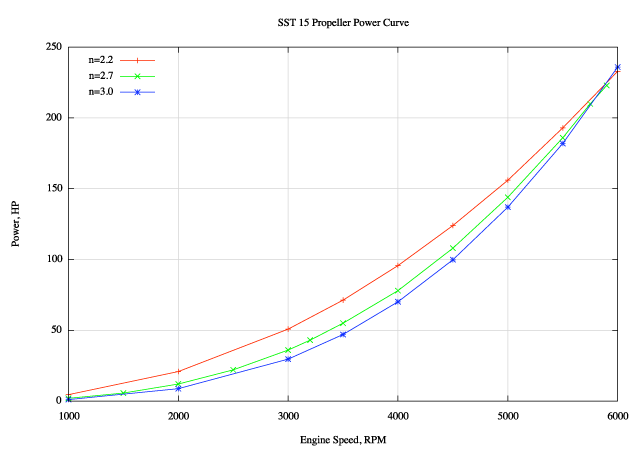
As you can see, it does not make a huge difference in the shape of the power curve.
I also developed some propeller power curves for two other propellers that I have tested and had some data on: the Mercury MIRAGEplus 17-inch pitch and the Mercury REVOLUTION4 17-inch pitch. The point where the propeller power curve crosses the engine power curve is the limit that the engine speed will reach, and these curves show the actual test results. (The engine was held to 5,400-RPM with the MIRAGE and to 4,700-RPM with the REVOLUTION4.)

The curves show that propellers which have greater pitch, and in the case of the REVOLUTION4 an additional blade, require more power to turn them. To show how much more power these propellers need, I expanded the plot to reach 6,000-RPM. As the propeller power curve shows, it takes a tremendous amount of power to turn a REVOLUTION4 17-pitch on my boat to 6,000-RPM.

You can operate the boat with these larger propellers, however, you see that there is not as much reserve power available, particularly with the four-blade. I have run the MIRAGEplus quite a bit, but generally when the boat is not heavily loaded and when I do not expect high dynamic loads as would be encountered in big seas. With those limitations, it does quite well, and the boat gets better fuel economy.
DISCLAIMER: This information is believed to be accurate but there is no guarantee. We do our best!
Copyright © 2007, 2018 by James W. Hebert. Unauthorized reproduction prohibited!
This is a verified HTML 4.0 document served to you from continuousWave
Author: James W. Hebert
This article first appeared January 13, 2008.